第一章Femap with NX Nastran基础
资料概况
| 更新时间:2015-06-29 | 下载次数: |
| 资料语言:简体中文 | 资料大小: 未知 |
| 下载来源: | 下载地址 |
资料介绍
第一章Femap with NX Nastran基础
1.1 CAE技术
CAE(Computer Aided Engineering)是用计算机辅助求解复杂工程和产品结构强度、刚度、屈曲稳定性、动力响应、热传导、多体接触、弹塑性等力学性能的分析计算以及结构性能的优化设计等问题的一种近似数值分析方法。CAE从60年代初在工程上开始应用到今天,经历了50多年的发展历史,其理论和算法经历了从蓬勃发展到日趋成熟的过程,已成为工程和产品结构分析中(如航空、航天、机械、土木结构等领域)必不可少的数值计算工具,同时也是分析连续力学各类问题的一种重要手段。随着计算机技术的普及和不断提高,CAE系统的功能和计算精度都得到大幅提高,各种基于产品数字建模的CAE系统应运而生,并已成为结构分析和 结构优化的重要工具,同时也是计算机辅助4C系统(CAD/CAE/CAPP/CAM)的重要环节。
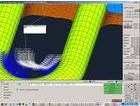
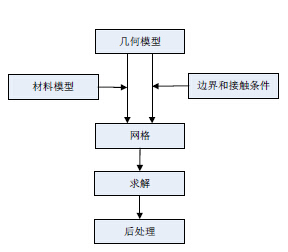
CAE技术主要包括前处理、解算和后处理三个环节。前处理是指:采用CAD技术建立CAE的几何模型和物理模型,完成分析数据的输入。后处理是对计算结果进行可视化处理,生成形象的图形输出,如位移图、应力、温度、压力分布的等值线图,表示应力、温度、压力分布的云图,以及随机械载荷和温度载荷变化生成位移、应力、温度、压力等分布动态图。根据经验,CAE各阶段所用的时间为:40%~45%用于模型的建立和数据输入,50%~55%用于分析结果的判读和评定,而真正的分析计算时间只占5%左右。
有限元法的基本过程是将一个形状复杂的连续求解区域分解为有限的形状简单的子域,即将一个连续体简化为由有限个单元组合的等效组合体,把求解连续体的场变量(应力、位移、压力和温度等)问题简化为求解有限的单元节点上的场变量值。此时得到的基本方程是一个代数方程组,而不是原来描述真实连续体场变量的微分方程组。最后,求解方程组后得到近似的数值解。数值解逼近真实值的程度取决于所采用的单元类型、数量以及对单元的插
1.1.1有限元技术
有限元法(FEA,Finite Element Analysis)的基本概念是用较简单问题代替复杂问题后再求解。它将求解域看成是由许多称为有限单元的互连子域组成,对每一单元假定一个合适的(较简单的)近似解,然后推导求解整个域的满足条件(如结构的平衡方程),从而得到问题的解。由于大多数实际问题难以得到准确解,而有限元法不仅计算精度高,而且能适应各种复杂形状,因而成为行之有效的工程分析手段。基于有限元方法的CAE系统的核心思想是结构的离散化,即将实际结构离散为有限数目的规则单元组合体,实际结构的物理性能可以通过对离散单元体进行分析,得出满足工程精度的近似结果来替代对实际结构的分析,从而解决理论分析无法解决的、复杂的、实际工程问题。
有限元法的基本过程是将一个形状复杂的连续求解区域分解为有限的形状简单的子域,即将一个连续体简化为由有限个单元组合的等效组合体,把求解连续体的场变量(应力、位移、压力和温度等)问题简化为求解有限的单元节点上的场变量值。此时得到的基本方程是一个代数方程组,而不是原来描述真实连续体场变量的微分方程组。最后,求解方程组后得到近似的数值解。数值解逼近真实值的程度取决于所采用的单元类型、数量以及对单元的插
2值函数等因素。
下载排行榜
-
STAR-CCM+介绍
下载:2127
- GeoStudio工程应用实例.. 1081
- TrueGrid-结构网格划分.. 1042
- STAR-CCM+在空调系统中.. 778
- ABAQUS动力分析资料 1711
- 基于ANSYS 的边坡开挖模拟 1201
- Ansys屈曲分析实例 1259
- Abaqus 6.10 安装指南 2365
- ABAQUS技巧积累 5927
- GeoStudio工程应用实例.. 918